Pedersen Hash¶
Contents
Scope¶
The 4-bit window Pedersen hash function is a secure hash function which maps a sequence of bits to a compressed point on an elliptic curve (Libert, Mouhartem, and Stehlé, n.d.).
This proposal aims to standardize this hash function for use primarily within the arithmetic circuits of zero knowledge proofs, together with other generic uses such as for Merkle tree or any use cases requiring a secure hash function.
As part of the standard, the paper details the elliptic curve used for the hash function, the process to compute the Pedersen hash from a given sequence of bits, and the computation of the hash from a sequences of bits using an arithmetic circuit—which can be used within zero knowledge proofs.
Moreover the paper includes references to open-source implementations of the Pedersen hash function which follows the computation process details in this proposal.
Motivation¶
The primary advantage of this Pedersen hash function is its efficiency. The ability to compute the hash efficiently makes it an attractive proposal for use within the circuits associated with zk-SNARK proofs (“ZCash Open Discussion: Choose Improved Hash Function for Merkle Tree (or Replace Merkle Tree),” n.d.).
Having a standard, secure, and efficient hash function is one of the paramount aspect for implementing usable, comprehensible, and easily verifiable zero knowledge proofs.
Background¶
The Pedersen hash has already been defined and used by the ZCash team in Sapling, their latest network upgrade (Hopwood et al., n.d.). They construct it on the Jubjub elliptic curve and using 3-bit lookup tables. In this document, we propose a different implementation of the Pedersen hash function using Baby-Jubjub elliptic curve and 4-bit windows, which requires less constraints per bit than using 3-bit windows.
Terminology¶
Elliptic Curve: Baby-Jubjub¶
Consider the prime number
\(p\) elements.
We define \(E_M\) as the Baby-Jubjub Montgomery elliptic curve defined over \(\ensuremath{\mathbb{F}_p}\) given by equation
subgroup of points of order \(r\), that is,
\[ \begin{align}\begin{aligned}E: x^2 + y^2 = 1 + d x^2 y^2\\where\end{aligned}\end{align} \]\(d = 9706598848417545097372247223557719406784115219466060233080913168975159366771.\)
\[ \begin{align}\begin{aligned}(x,y) \to (u,v) = \left( \frac{1 + y}{1 - y} , \frac{1 + y}{(1 - y)x} \right)\\with inverse from :math:`E_M` to :math:`E`\end{aligned}\end{align} \]\[(u, v) \to (x, y) = \left( \frac{u}{v}, \frac{u - 1}{u + 1} \right).\]
Pedersen Hash¶
Let \(M\) be a sequence of bits. The Pedersen hash function of \(M\) is defined as follows:
Let \(P_0,P_1,\dots,P_k\) be uniformly sampled generators of \(\ensuremath{\mathbb{G}}\) (for some specified integer \(k\)).
Split \(M\) into sequences of at most 200 bits and each of those into chunks of 4 bits [1]. More precisely, write
\[ \begin{align}\begin{aligned}\begin{split} \begin{gathered} M = M_0M_1\dots M_l \quad\text{where}\quad M_i = m_0m_1\dots m_{k_i} \quad\text{with}\quad \begin{cases} k_i = 49 \;\text{ for } i = 0, \dots, l-1, \\ k_i \leq 49 \;\text{ for } i = l, \end{cases} \end{gathered}\end{split}\\where the :math:`m_j` terms are chunks of 4 bits\end{aligned}\end{align} \]\([b_0\: b_1\: b_2\: b_3]\). Define
\[ \begin{align}\begin{aligned} enc(m_j) = (2b_3-1) \cdot (1+b_{0}+2b_{1}+4b_{2})\\and let\end{aligned}\end{align} \]\[ \begin{align}\begin{aligned}\langle M_i \rangle = \sum_{j=0}^{k_i-1} enc(m_j) \cdot 2^{5j}.\\We define the Pedersen hash of :math:`M` as\end{aligned}\end{align} \]\[ \begin{align}\begin{aligned} \label{eq-ped} H(M) = \langle M_0 \rangle \cdot P_0 + \langle M_1 \rangle \cdot P_1 + \langle M_2 \rangle \cdot P_2 + \dots + \langle M_l \rangle \cdot P_l.\\Note that the expression above is a linear combination of elements\end{aligned}\end{align} \]of \(\ensuremath{\mathbb{G}}\), so itself is also an element of \(\ensuremath{\mathbb{G}}\). That is, the resulting Pedersen hash \(H(M)\) is a point of the elliptic curve \(E\) of order \(r\).
Description¶
Set Of Generators¶
We generate the points \(P_0,\dots,P_{{k}}\) in such a manner that
it is difficult to find a connection between any of these two points.
More precisely, we take D = "string\_seed" followed by a byte S
holding that smallest number that H = Keccak256(D || S) results in a
point in the elliptic curve \(E\).
Computation Of The Pedersen Hash¶
In the following circuit pedersen hash, we have depicted the circuit used to compute the Pedersen hash of a message \(M\) described in equation [eq-ped]. Each multiplication box returns a term of the sum.
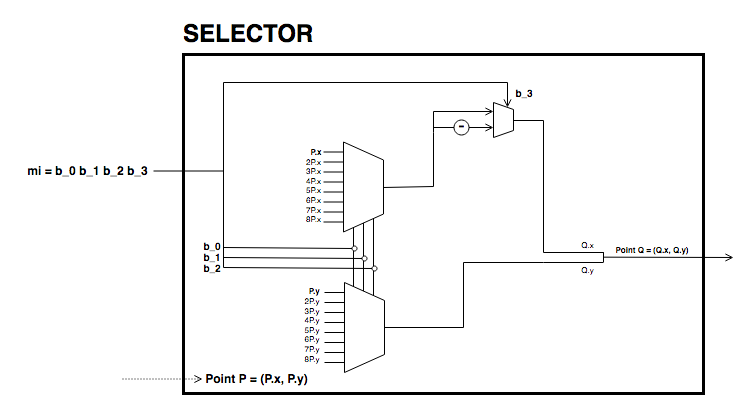

As the set of generators are fixed, we can precompute its multiples and use 4-bit lookup windows to select the right points. This is done as shown in the circuit called selector. This circuit receives 4-bit chunk input and returns a point. The first three bits are used to select the right multiple of the point and last bit decides the sign of the point. The sign determines if the \(x\)-coordinate should be taken positive or negative, as with Edwards curves, negating a point corresponds to the negation of its first coordinate.

[sec-computation]
Examples And Test Vectors¶
Work In Progress
Challenges¶
One of the main challenges to create this standard and to see it adopted by the community is to provide correct, usable, and well-maintained implementations in as many languages as possible.
Some effort is also required to audit and verify code coming from the community and claiming to implement the 4-bit window Pedersen hash function to prevent the propagation of potentially insecure implementations.
Finally, the proposal as it stands today includes the padding of the message \(M\) to a multiple of four bits. There are potentials issues with this approach where collisions can happen.
Security¶
Overflow Prevention¶
\[ \begin{align}\begin{aligned}n = 2^0 \times8 + 2^5 \times 8 + \left(2^5\right)^2 \times8 \dots + 2^{245}\times 8 .\\To avoid overflow, this number should be smaller than\end{aligned}\end{align} \]\((r-1)/2\). Indeed,
\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} \quad\; n & = 8 \times \sum_{ k = 0}^{49} 2^{5k} = 8 \times \frac{2^{250}-1}{2^5-1}\\ & = 466903585634339497675689455680193176827701551071131306610716064548036813064%\\\end{aligned}\end{split}\\and\end{aligned}\end{align} \]\[\begin{split}\begin{aligned} \frac{r-1}{2} &= 1368015179489954701390400359078579693038406986079283629600107830474223686520 \\ & > n.\\ \vspace{0.4cm}\end{aligned}\end{split}\]
Implementation¶
A Note On Efficency: Number Of Constraints Per Bit¶
- 3-lookup window : \((1+3+2)/3 = 2\) constraints per bit.
- 4-lookup window : \((1 +3+3)/4 = 1.75\) constraints per bit.
The specific constraints can be determined as follows: let the multiplexers of coordinates \(x\) and \(y\) be represented by the following look up tables:
| \(s_2\) | \(s_1\) | \(s_0\) | \(out\) |
|---|---|---|---|
| 0 | 0 | 0 | \(a_0\) |
| 0 | 0 | 1 | \(a_1\) |
| 0 | 1 | 0 | \(a_2\) |
| 0 | 1 | 1 | \(a_3\) |
| 1 | 0 | 0 | \(a_4\) |
| 1 | 0 | 1 | \(a_5\) |
| 1 | 1 | 0 | \(a_6\) |
| 1 | 1 | 1 | \(a_7\) |
| \(s_2\) | \(s_1\) | \(s_0\) | \(out\) |
|---|---|---|---|
| 0 | 0 | 0 | \(b_0\) |
| 0 | 0 | 1 | \(b_1\) |
| 0 | 1 | 0 | \(b_2\) |
| 0 | 1 | 1 | \(b_3\) |
| 1 | 0 | 0 | \(b_4\) |
| 1 | 0 | 1 | \(b_5\) |
| 1 | 1 | 0 | \(b_6\) |
| 1 | 1 | 1 | \(b_7\) |
We can express them with the following 3 constraints:
\(aux = s_0 s_1\)
- \(out = [ (a_7-a_6-a_5+a_4-a_3+a_2+a_1-a_0)*aux + (a_6-a_4-a_2+a_0)*s_1\)\(\text{\qquad\;\;} + (a_5-a_4-a_1+a_0)*s_0 + (a_4 - a_0) ] z + (a_3-a_2-a_1+a_0)*aux + (a_2-a_0)*s_1\)\(\text{\qquad\;\;} + (a_1-a_0)*s_0+ a_0\)
- \(out = [ (b_7-b_6-b_5+b_4-b_3+b_2+b_1-b_0)*aux + (b_6-b_4-b_2+b_0)*s_1\)\(\text{\qquad\;\;} + (b_5-b_4-b_1+b_0)*s_0 + (b_4 - b_0)] z + (b_3-b_2-b_1+b_0)*aux + (b_2-b_0)*s_1 \\ \text{\qquad\;\:} + (b_1-b_0)*s_0+ b_0\)
Existing Implementations¶
Implementation of the specifications and arithmetic of the Baby-Jubjub curve:
- Barry WhiteHat (SAGE): https://github.com/barryWhiteHat/baby_jubjub.
- Jordi Baylina (circom language): https://github.com/iden3/circomlib/blob/master/circuits/babyjub.circom.
Implementation of the Pedersen Hash function:
- Jordi Baylina (circom language): https://github.com/iden3/circomlib/blob/master/circuits/.
Intellectual Property¶
The source code of the implementations listed in this proposal are publicly available. Circom is licensed under GPL3.
Bernstein, Daniel J., Peter Birkner, Marc Joye, Tanja Lange, and Christiane Peters. n.d. “Twisted Edwards Curves.” Cryptology ePrint Archive, Report 2008/013.
Hopwood, Daira, Sean Bowe, Taylor Hornby, and Nathan Wilcox. n.d. “ZCash Protocol Specification Version 2018.0-Beta-31.”
Libert, B., F. Mouhartem, and D. Stehlé. n.d. “Tutorial 8.”
“ZCash Open Discussion: Choose Improved Hash Function for Merkle Tree (or Replace Merkle Tree).” n.d.
| [1] | If \(M\) is not a multiple of 4, pad \(M\) to a multiple of 4 bits by appending zero bits. |