Merkle Tree¶
Contents
Scope¶
A Merkle tree or hash tree is an authenticated data structure where every leaf node of the tree contains the cryptographic hash of a data block and every non leaf node contains the concatenated hashes of its child nodes (Haider 2018). If the majority of the leaves are empty, then they are called sparse Merkle trees (Dahlberg, Pulls, and Peeters 2016). This proposal aims to standardize the generation of this second kind of binary trees.
Motivation¶
Merkle trees allow to link a set of data to a unique has value, which is very optimal and useful, specially in blockchain technology, as it provides a secure and efficient verification of large data sets by storing only a little piece of data on-chain. For instance, they can be used to verify any kind of data stored, handled and transferred in and between computers. They can help ensure that data blocks received from other peers in a peer-to-peer network are received undamaged and unaltered, and even to check that the other peers do not lie and send fake blocks (Wikipedians, n.d.).
Background¶
We are still working on the literature compending the state of the art of this area.
Terminology¶
The following concepts are definitions and properties we assume across the document.
- The leaves of the Merkle tree consist of key-value pairs
\((k,v)\). We distinguish three different nodes:
- Empty node: A vertex that stores the key and value zero.
- Leaf: A vertex with both empty children.
- Internal node: A vertex with at least one non-empty child. The value is and the key such. It has the hash of its children.
- A Merkle audit path for a leaf in a Merkle tree is the shortest list of additional nodes in the tree required to compute the root hash for that tree.
- If the root computed from the audit path matches the true root, then the audit path is a proof of membership for that leaf in the tree.
- Otherwise, it is a proof of non-membership for that leaf in the tree.
Challenges¶
Work in progress.
Description¶
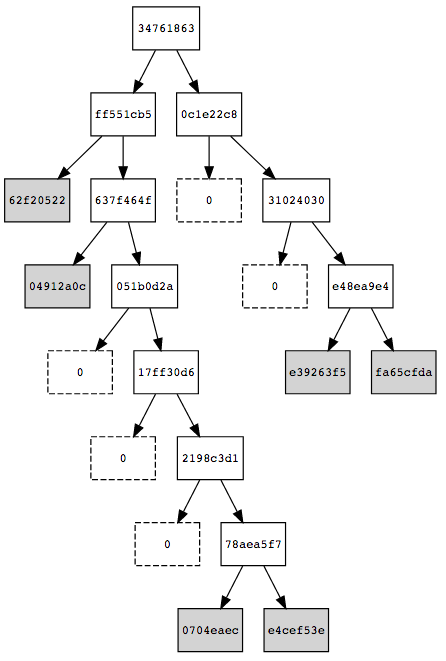
\[ \begin{align}\begin{aligned}H_{path} = H(e) = H(1 || k || v).\\This array of bits is going to represent a path through the tree:\end{aligned}\end{align} \]starting by the less significant bit and from the root of \(T\), it descents the tree by taking the left edge if there is a 0 and right one if there is a 1.

If we go down the tree following the sequence 01111111… we get to the leaf containing the value 0704eaec of some \(e'\) with \(H'_{path}=0111110...\) . Comparing \(H_{path}\) and \(H'_{path}\), the 7th bit is the first different bit. This means, that we should go down to the 7th level and store there the entries as shown in next figure:

- Each leaf consists of a pair (\(H(1 || k || v)\), \(k||v\)).
- Each intermediate node of a pair (\(H(H_L||H_R)\), \(K_L||K_R\)), where \((H_L,K_L)\) is the key-value of its left child and \((H_L,K_L)\) the key-value of its right child.
\(H_{path} \gets \text{GetPath($e$)}\) \(b \gets \text{LeastSignificantBit($H_{Index}$)}\) \(r \gets e\) \(r \gets e\) \(H_{Index} \gets H_{Index}\backslash{b}\) \(b \gets \text{LeastSignificantBit($H_{Index}$)}\) \(e' \gets \text{GetEntryStoredIn($r$)}\) \(H'_{path} \gets \text{GetPath($e'$)}\) Find first bit \(b_j\) such that \(H_{path}(j) \not= H'_{path}(j)\) Leaf(\(b_0...b_j\))\(\gets e\) Leaf(\(b_0...b'_j\))\(\gets e'\) RecalculateIntermediateNodeValues(\(T\))
Security¶
The security of an audit path reduces to the collision resistance of the underlying hash function. For a proof, see (Dahlberg, Pulls, and Peeters 2016 Lemma 1).
Implementation¶
The standarisation of Merkle trees we proposed are described an implemented in GoLang and JavaScript by the iden3 team in the following repositories:
Some detailed examples are also provided in these repositories:
Intellectual Property¶
We will release the final version of this proposal under creative commons, to ensure it is freely available to everyone.
Dahlberg, Rasmus, Tobias Pulls, and Roel Peeters. 2016. “Efficient Sparse Merkle Trees: Caching Strategies and Secure (Non-)Membership Proofs.” Cryptology ePrint Archive, Report 2016/683.
Haider, Faraz. 2018. “Compact Sparse Merkle Trees.” Cryptology ePrint Archive, Report 2018/955.
Wikipedians, B. n.d. Data Structures. PediaPress. https://books.google.es/books?id=aYxSZurAGXEC.
| [1] | If the hash function \(H\) does not return a binary number, binarize it later. |