Baby Jubjub¶
Contents
1.2
Scope¶
This proposal aims to define a specific elliptic curve defined over the large prime subgroup of BN128 elliptic curve.
Motivation¶
The search for this elliptic curve defined is motivated by its usefulness in zk-SNARK proofs. Moreover the ability to find it in a deterministic way—so that it was clear no other considerations were taken for defining—is paramount as it significantly reduces the possibility of a backdoor being present, thus leading to better security.
Background¶
With this purpose, we used a deterministic algorithm for finding elliptic curves over a specified finite field (Langley, Hamburg, and Turner, n.d.) together with the restrictions of security parameters described in SafeCurves project (Bernstein and Lange, n.d.).
Terminology And Description¶
Generation Of Baby Jubjub¶
Definition Of Baby Jubjub¶
From now on, let
elements.
Montgomery Form¶
We define \(E_M\) as the Baby-Jubjub Montgomery elliptic curve defined over \(\ensuremath{\mathbb{F}_p}\) given by equation
subgroup of points of order \(r\), that is,
Edwards Form¶
\[ \begin{align}\begin{aligned}E: x^2 + y^2 = 1 + d x^2 y^2\\where\end{aligned}\end{align} \]\(d = 9706598848417545097372247223557719406784115219466060233080913168975159366771.\)
\[ \begin{align}\begin{aligned}(x,y) \to (u,v) = \left( \frac{1 + y}{1 - y} , \frac{1 + y}{(1 - y)x} \right)\\with inverse from :math:`E_M` to :math:`E`\end{aligned}\end{align} \]\[(u, v) \to (x, y) = \left( \frac{u}{v}, \frac{u - 1}{u + 1} \right).\]
Arithmetic In Baby Jubjub¶
In this section we define how to operate in the elliptic curve group: the addition of points and multiplication of a point by a scalar (an element of \(\ensuremath{\mathbb{F}_p}\)).
Addition Of Points¶
When adding points of elliptic curves in Montgomery form, one has to be careful if the points being added are equal (doubling) or not (adding) and if one of the points is the point at infinity (Okeya, Kurumatani, and Sakurai 2000). Edwards curves have the advantage that there is no such case distinction and doubling can be performed with exactly the same formula as addition (Bernstein et al., n.d.). In comparison, operating in Montgomery curves is cheaper. In this section, we summarize how addition and doubling is performed in both forms. For the exact number of operations required in different forms of elliptic curves, see (Bernstein et al., n.d.).
: Let \(P_{1} = (x_{1}, y_{1})\) and \(P_{2} = (x_{2}, y_{2})\) be points of the Baby-Jubjub twisted Edwards elliptic curve \(E\). The sum \(P_1 + P_2\) is a third point \(P_3 = (x_3, y_3)\) with
\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} &\lambda = d x_1x_2y_1y_2,\\ &x_3 = (x_1y_2 + y_1x_2) / (1 + \lambda),\\ &y_3 = (y_1y_2 - x_1x_2) / (1 - \lambda). \end{aligned}\end{split}\\Note that the neutral element is the point :math:`O = (0,1)` and the\end{aligned}\end{align} \]inverse of a point \((x,y)\) is \((-x,y)\).
: Let \(P_{1} = (x_{1}, y_{1})\not=O\) and \(P_{2} = (x_{2}, y_{2})\not=O\) be two points of the Baby-JubJub elliptic curve \(E_M\) in Montgomery form.
If \(P_1\not=P_2\), then the sum \(P_1 + P_2\) is a third point \(P_3 = (x_3, y_3)\) with coordinates
\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} \label{eq-ted} \begin{split} &\Lambda = (y_2-y_1)/ (x_2-x_1),\\ &x_3 = \Lambda^2 - A - x_1 - x_2,\\ &y_3 = \Lambda(x_1- x_3) - y_1. \end{split} \end{aligned}\end{split}\\If :math:`P_1 = P_2`, then :math:`2\cdot P_1` is a point\end{aligned}\end{align} \]\(P_3 = (x_3, y_3)\) with coordinates
\[\begin{split}\begin{aligned} \label{eq-mont} \begin{split} &\Lambda = (3x_1^2 + 2Ax_1 + 1)/ (2y_1),\\ &x_3 = \Lambda^2 - A - 2x_1,\\ &y_3 = \Lambda(x_1- x_3) - y_1. \end{split} \end{aligned}\end{split}\]
Multiplication Of A Point Of \(E\) By A Scalar¶
Let \(P\not= O\) be a point of the Edwards curve \(E\) of order strictly greater than 8 (i.e. \(P\in\ensuremath{\mathbb{G}}\)) and let \(k\) a binary number representing an element of \(\ensuremath{\mathbb{F}_p}\). We describe the circuit used to compute the point \(k\cdot P\).
First, we divide \(k\) into chunks of 248 bits. If \(k\) is not a multiple of 248, we take \(j\) segments of 248 bits and leave a last chunk with the remaining bits. More precisly, write
\[ \begin{align}\begin{aligned}\begin{split} \begin{gathered} k = k_0 k_1 \dots k_j \quad\text{with}\quad \begin{cases} k_i = b^i_0 b^i_1 \dots b^i_{247} \;\text{ for } i = 0, \dots, j-1, \\ k_j = b^j_0 b^j_1 \dots b^j_s \;\text{ with } s\leq 247. \end{cases} \end{gathered}\end{split}\\Then,\end{aligned}\end{align} \]\[ \begin{align}\begin{aligned} \label{kP} k\cdot P = k_0\cdot P + k_1\cdot 2^{248}P +\dots+ k_j\cdot 2^{248j}P.\\This sum is done using the following circuit. The terms of the sum\end{aligned}\end{align} \]are calculated separately inside the seq boxes and then added together.
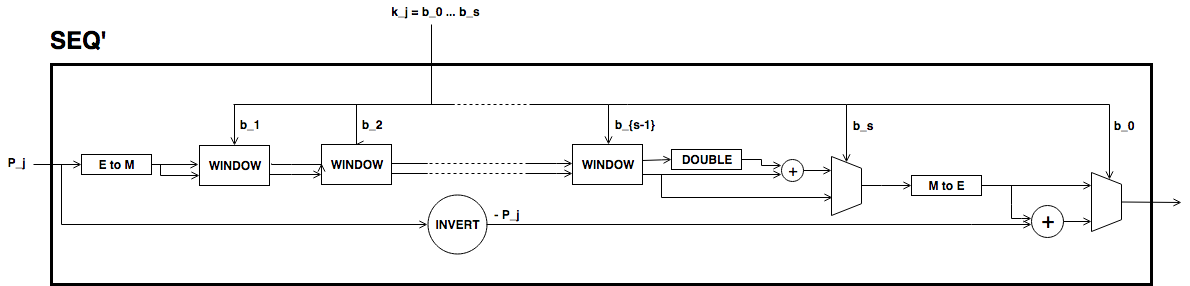
Each seq box takes a point of \(E\) of the from \(P_i = 2^{248 i} P\) for \(i=0,\dots,j-1\) and outputs two points
\[ \begin{align}\begin{aligned} 2^{248} \cdot P_i \quad \text{and} \quad \sum_{n = 0}^{247} b_n \cdot 2^{n} \cdot P_i.\\The first point is the input of the next :math:`(i+1)`-th seq box\end{aligned}\end{align} \](note that \(2^{248} \cdot P_i = P_{i+1}\)) whereas the second output is the computation of the \(i\)-th term in expression ([kP]). The precise circuit is depicted in next two figures seq and window.


The idea of the circuit is to first compute
\[ \begin{align}\begin{aligned} Q = P_i + b_1 \cdot (2P_i) + b_2 \cdot (4P_i) + b_3 \cdot (8P_i) + \dots + b_{247} \cdot (2^{247}P_i),\\and output the point\end{aligned}\end{align} \]\[ \begin{align}\begin{aligned}Q - b_0 \cdot P_i.\\This permits the computation of :math:`Q` using the Montgomery form\end{aligned}\end{align} \]of Baby-Jubjub and only use twisted Edwards for the second calculation. The reason to change forms is that, in the calculation of the output, we may get a sum with input the point at infinity if \(b_0 = 0\).
Still, we have to ensure that none of the points being doubled or added when working in \(E_M\) is the point at infinity and that we never add the same two points.
- By assumption, \(P\not= O\) and ord\((P)>8\). Hence, by Lagrange theorem (Baumslag and Chandler 1968 Corollary 4.12), \(P\) must have order \(r\), \(2r\), \(4r\) or \(8r\). For this reason, none of the points in \(E_M\) being doubled or added in the circuit is the point at infinity, because for any integer \(m\), \(2^m\) is never a multiple of \(r\), even when \(2^m\) is larger than \(r\), as \(r\) is a prime number. Hence, \(2^m \cdot P \not= O\) for any \(m\in\ensuremath{\mathbb{Z}}\).
- Looking closely at the two inputs of the sum, it is easy to realize that they have different parity, one is an even multiple of \(P_i\) and the other an odd multiple of \(P_i\), so they must be different points. Hence, the sum in \(E_M\) is done correctly.
The last term of expression ([kP]) is computed in a very similar manner. The difference is that the number of bits composing \(k_j\) may be shorter and that there is no need to compute \(P_{j+1}\), as there is no other seq box after this one. So, there is only output, the point \(k_j \cdot P_j = k_j\cdot 2^{248j} P\). This circuit is named seq’.

Challenges And Security¶
As required in the construction of Baby-Jubjub, the curve satisfies SafeCurves criteria. This can be checked following (Hat, n.d.).
Implementation¶
Barry WhiteHat:
Jordi Baylina: https://github.com/iden3/circomlib/blob/master/src/babyjub.js
Intellectual Property¶
We will release the final version of this proposal under creative commons, to ensure it is freely available to everyone.
Baumslag, Benjamin, and Bruce Chandler. 1968. Schaum’s Outline of Theory and Problems of Group Theory. Schaum’s Outline Series. New York: McGraw-Hill Book Company.
Bernstein, Daniel J., Peter Birkner, Marc Joye, Tanja Lange, and Christiane Peters. n.d. “Twisted Edwards Curves.” Cryptology ePrint Archive, Report 2008/013.
Bernstein, Daniel J., and Tanja Lange. n.d. “SafeCurves: Choosing Safe Curves for Elliptic-Curve Cryptography.”
Hat, Barry White. n.d. “Baby-Jubjub Supporting Evidence.” GitHub.
Langley, Adam, Mike Hamburg, and Sean Turner. n.d. “Elliptic Curves for Security.” Request for Comments. RFC 7748; RFC Editor. https://doi.org/10.17487/RFC7748.
Okeya, Katsuyuki, Hiroyuki Kurumatani, and Kouichi Sakurai. 2000. “Elliptic Curves with the Montgomery-Form and Their Cryptographic Applications.” In Proceedings of the Third International Workshop on Practice and Theory in Public Key Cryptography: Public Key Cryptography, 238–57. PKC ’00. London, UK, UK: Springer-Verlag. http://dl.acm.org/citation.cfm?id=648117.746614.