ED-DSA¶
Contents
1.2
Scope¶
This proposal aims to standarize the elliptic curve signature scheme Edwards-curve Digital Signature Algorithm (EdDSA) for Baby Jubjub Edwards elliptic curve using MiMC-7 hash function.
Motivation¶
EdDSA is a variant of Schnorr’s signature scheme and it provides high performance on a variety of platforms (Josefsson and Liusvaara, n.d.).
Background¶
Terminology¶
The table below summarizes the terminology used across the document. Each element is explained in greater detail in the following sections.
| Notation | Description |
|---|---|
| \(p\) | Prime number. |
| \(\ensuremath{\mathbb{F}_p}\) | Finite field with \(p\) elements. |
| \(E\) | Baby Jubjub elliptic curve (defined over \(Fp\)) in Edwards form. |
| \(E_M\) | Baby Jubjub elliptic curve (defined over \(Fp\)) in Montgomery form. |
| \(l\) | Large prime number dividing the order of Baby Jubjub. |
| \(\ensuremath{\mathbb{F}_l}\) | Finite field with \(l\) elements. |
| \(\ensuremath{\mathbb{G}}\) | Group of \(\ensuremath{\mathbb{F}_p}\) -rational points of order \(l\). |
| \(B\) | Base point (generator of \(\ensuremath{\mathbb{G}}\)) of Baby Jubjub. |
| \(A = (A_x, A_y)\) | Public key. \(A\) is a point on \(E\). |
| \(k\) | Private key. |
| \(M\) | Message. \(M\) is an element of \(\ensuremath{\mathbb{F}_l}\) . |
| \((R,S) = ((R_x, R_y), S)\) | Signature on \(M\). \(R\) is a point on \(E\) and \(S\) and element of \(\ensuremath{\mathbb{F}_l}\) . |
| \(H\) | Hash function MiMC-7. |
| \(r\) | Number of rounds of MiMC-7. |
| \(c_0, c_1, \dots, c_r\) | Constants used in MiMC-7. |
[tab:notation]
Baby-Jubjub¶
\[ \begin{align}\begin{aligned} p = 21888242871839275222246405745257275088548364 400416034343698204186575808495617\\and let :math:`\ensuremath{\mathbb{F}_p}` be the finite field with\end{aligned}\end{align} \]\(p\) elements. We define \(E_M\) as the Baby-Jubjub Montgomery elliptic curve defined over \(\ensuremath{\mathbb{F}_p}\) given by equation
\[ \begin{align}\begin{aligned}E: v^2 = u^3 + 168698u^2 + u.\\The order of :math:`E_M` is :math:`n = 8\times l`, where\end{aligned}\end{align} \]\[ \begin{align}\begin{aligned} l = 2736030358979909402780800718157159386076813972 158567259200215660948447373041\\is a prime number. Denote by :math:`\ensuremath{\mathbb{G}}` the\end{aligned}\end{align} \]subgroup of points of order \(l\), that is,
\[ \begin{align}\begin{aligned}\ensuremath{\mathbb{G}}= \Set{ P \in E(\ensuremath{\mathbb{F}_p}) | l P = O }.\\Let\end{aligned}\end{align} \]\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} B = (17777552123799933955779906779655732241715742912184938656739573121738514868268,\\ 2626589144620713026669568689430873010625803728049924121243784502389097019475)\end{aligned}\end{split}\\be a generator of :math:`\ensuremath{\mathbb{G}}`.\end{aligned}\end{align} \]
\[ \begin{align}\begin{aligned}E: x^2 + y^2 = 1 + d x^2 y^2\\where\end{aligned}\end{align} \]\(d = 9706598848417545097372247223557719406784115219466060233080913168975159366771.\)
\[ \begin{align}\begin{aligned}(x,y) \to (u,v) = \left( \frac{1 + y}{1 - y} , \frac{1 + y}{(1 - y)x} \right)\\with inverse from :math:`E_M` to :math:`E`\end{aligned}\end{align} \]\[(u, v) \to (x, y) = \left( \frac{u}{v}, \frac{u - 1}{u + 1} \right).\]
MiMC-7¶
\[E_k(x) = (F_{r-1} \circ F_{r-2} \circ ... \circ F_0)(x) \oplus k.\]
= [draw, minimum size=2em] = [pin edge=to-,thin,black]
As the random constants \(c_i\) do not need to be generated for every evaluation of MiMC-7, they are hard-coded into the implementation. The generation of these constants and the required number of rounds is described in section 6.2.
EdDSA¶
The description of this protocol is based in (Josefsson and Liusvaara, n.d.): Let the public key be a point \(A = (A_x, A_y)\in E\) of order \(l\) and \(M\) a message we wish to sign. The signature on \(M\) by \(A\) consists of a par \((R,S)\) where \(R = (R_x, R_y)\) is a point of order \(l\) of \(E\) and \(S\in\ensuremath{\mathbb{F}_l}\backslash\{0\}\) such that
Challenges and security¶
One of the main challenges to create this standard and to see it adopted by the community is to provide correct, usable, and well-maintained implementations in as many languages as possible. Some effort is also required to audit and verify code coming from the community and claiming to implement EdDSA for Baby Jubjub to prevent the propagation of potentially insecure implementations. Part of the work in progress of looking batch verification of short signatures. Lastly, the proposal as it stands uses MiMC-7 as hash function as it works very optimal inside circuits. We believe some work is required to determinate the security MiMC hash functions.
Implementation¶
In this section, we specify how each of the main operations in the following EdDSA circuit are computed:
Operations in the elliptic curve¶
Addition of points¶
When adding points of elliptic curves in Montgomery form, one has to be careful if the points being added are equal (doubling) or not (adding) and if one of the points is the point at infinity (Okeya, Kurumatani, and Sakurai 2000). Edwards curves have the advantage that there is no such case distinction and doubling can be performed with exactly the same formula as addition (Bernstein et al., n.d.). In comparison, operating in Montgomery curves is cheaper. In this section, we summarize how addition and doubling is performed in both forms. For the exact number of operations required in different forms of elliptic curves, see (Bernstein et al., n.d.).
: Let \(P_{1} = (x_{1}, y_{1})\) and \(P_{2} = (x_{2}, y_{2})\) be points of the Baby-Jubjub twisted Edwards elliptic curve \(E\). The sum \(P_1 + P_2\) is a third point \(P_3 = (x_3, y_3)\) with
\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} &\lambda = d x_1x_2y_1y_2,\\ &x_3 = (x_1y_2 + y_1x_2) / (1 + \lambda),\\ &y_3 = (y_1y_2 - x_1x_2) / (1 - \lambda). \end{aligned}\end{split}\\Note that the neutral element is the point :math:`O = (0,1)` and the\end{aligned}\end{align} \]inverse of a point \((x,y)\) is \((-x,y)\).
: Let \(P_{1} = (x_{1}, y_{1})\not=O\) and \(P_{2} = (x_{2}, y_{2})\not=O\) be two points of the Baby-JubJub elliptic curve \(E_M\) in Montgomery form.
If \(P_1\not=P_2\), then the sum \(P_1 + P_2\) is a third point \(P_3 = (x_3, y_3)\) with coordinates
\[ \begin{align}\begin{aligned}\begin{split} \begin{aligned} \label{eq-ted} \begin{split} &\Lambda = (y_2-y_1)/ (x_2-x_1),\\ &x_3 = \Lambda^2 - A - x_1 - x_2,\\ &y_3 = \Lambda(x_1- x_3) - y_1. \end{split} \end{aligned}\end{split}\\If :math:`P_1 = P_2`, then :math:`2\cdot P_1` is a point\end{aligned}\end{align} \]\(P_3 = (x_3, y_3)\) with coordinates
\[\begin{split}\begin{aligned} \label{eq-mont} \begin{split} &\Lambda = (3x_1^2 + 2Ax_1 + 1)/ (2y_1),\\ &x_3 = \Lambda^2 - A - 2x_1,\\ &y_3 = \Lambda(x_1- x_3) - y_1. \end{split} \end{aligned}\end{split}\]
Multiplication of a point of \(E\) by a scalar¶
Let \(P\not= O\) be a point of the Edwards curve \(E\) of order strictly greater than 8 (i.e. \(P\in\ensuremath{\mathbb{G}}\)) and let \(k\) a binary number representing an element of \(\ensuremath{\mathbb{F}_p}\). We describe the circuit used to compute the point \(k\cdot P\).
First, we divide \(k\) into chunks of 248 bits. If \(k\) is not a multiple of 248, we take \(j\) segments of 248 bits and leave a last chunk with the remaining bits. More precisly, write
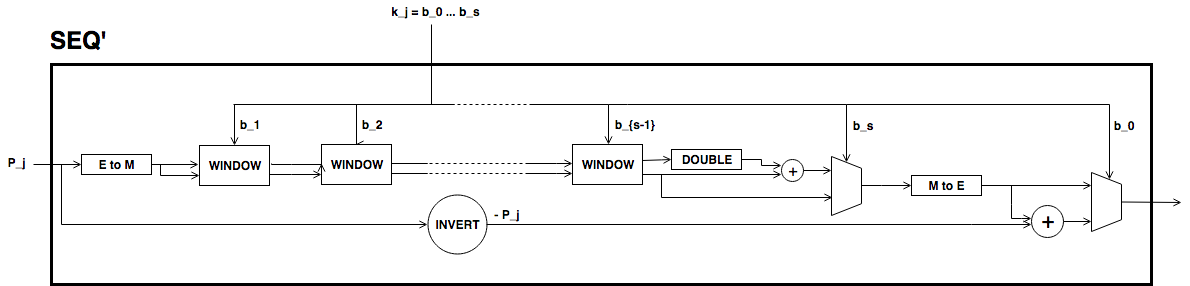
\[ \begin{align}\begin{aligned}\begin{split} \begin{gathered} k = k_0 k_1 \dots k_j \quad\text{with}\quad \begin{cases} k_i = b^i_0 b^i_1 \dots b^i_{247} \;\text{ for } i = 0, \dots, j-1, \\ k_j = b^j_0 b^j_1 \dots b^j_s \;\text{ with } s\leq 247. \end{cases} \end{gathered}\end{split}\\Then,\end{aligned}\end{align} \]\[ \begin{align}\begin{aligned} \label{kP} k\cdot P = k_0\cdot P + k_1\cdot 2^{248}P +\dots+ k_j\cdot 2^{248j}P.\\This sum is done using the following circuit. The terms of the sum\end{aligned}\end{align} \]are calculated separately inside the seq boxes and then added together.

Each seq box takes a point of \(E\) of the from \(P_i = 2^{248 i} P\) for \(i=0,\dots,j-1\) and outputs two points
\[ \begin{align}\begin{aligned} 2^{248} \cdot P_i \quad \text{and} \quad \sum_{n = 0}^{247} b_n \cdot 2^{n} \cdot P_i.\\The first point is the input of the next :math:`(i+1)`-th seq box\end{aligned}\end{align} \](note that \(2^{248} \cdot P_i = P_{i+1}\)) whereas the second output is the computation of the \(i\)-th term in expression ([kP]). The precise circuit is depicted in next two figures seq and window.


The idea of the circuit is to first compute
\[ \begin{align}\begin{aligned} Q = P_i + b_1 \cdot (2P_i) + b_2 \cdot (4P_i) + b_3 \cdot (8P_i) + \dots + b_{247} \cdot (2^{247}P_i),\\and output the point\end{aligned}\end{align} \]\[ \begin{align}\begin{aligned}Q - b_0 \cdot P_i.\\This permits the computation of :math:`Q` using the Montgomery form\end{aligned}\end{align} \]of Baby-Jubjub and only use twisted Edwards for the second calculation. The reason to change forms is that, in the calculation of the output, we may get a sum with input the point at infinity if \(b_0 = 0\).
Still, we have to ensure that none of the points being doubled or added when working in \(E_M\) is the point at infinity and that we never add the same two points.
- By assumption, \(P\not= O\) and ord\((P)>8\). Hence, by Lagrange theorem (Baumslag and Chandler 1968 Corollary 4.12), \(P\) must have order \(r\), \(2r\), \(4r\) or \(8r\). For this reason, none of the points in \(E_M\) being doubled or added in the circuit is the point at infinity, because for any integer \(m\), \(2^m\) is never a multiple of \(r\), even when \(2^m\) is larger than \(r\), as \(r\) is a prime number. Hence, \(2^m \cdot P \not= O\) for any \(m\in\ensuremath{\mathbb{Z}}\).
- Looking closely at the two inputs of the sum, it is easy to realize that they have different parity, one is an even multiple of \(P_i\) and the other an odd multiple of \(P_i\), so they must be different points. Hence, the sum in \(E_M\) is done correctly.
The last term of expression ([kP]) is computed in a very similar manner. The difference is that the number of bits composing \(k_j\) may be shorter and that there is no need to compute \(P_{j+1}\), as there is no other seq box after this one. So, there is only output, the point \(k_j \cdot P_j = k_j\cdot 2^{248j} P\). This circuit is named seq’.

MiMC-7¶
The specifications we use in the hash are (we are working in explaining this section in greater detail):
- Number of rounds: \(r = \ceil*{\frac{\log_2l}{\log_27}} = 91.\)
- Inputs:
- Coordinates of the public key: (\(A_x, A_y\)).
- Coordinates of the point \(8R\): (\(R8_x, R8_y\)).
- Message \(M\).
- Number of inputs: 5.
- Generation of constants: https://github.com/iden3/circomlib/blob/master/src/mimc7.js.
Example and test vectors¶
Work in progress.
Existing implementations¶
Intellectual Property¶
We will release the final version of this proposal under creative commons, to ensure it is freely available to everyone.
Albrecht, Martin, Lorenzo Grassi, Christian Rechberger, Arnab Roy, and Tyge Tiessen. 2016. “MiMC: Efficient Encryption and Cryptographic Hashing with Minimal Multiplicative Complexity.” Cryptology ePrint Archive, Report 2016/492.
Baumslag, Benjamin, and Bruce Chandler. 1968. Schaum’s Outline of Theory and Problems of Group Theory. Schaum’s Outline Series. New York: McGraw-Hill Book Company.
Bernstein, Daniel J., Peter Birkner, Marc Joye, Tanja Lange, and Christiane Peters. n.d. “Twisted Edwards Curves.” Cryptology ePrint Archive, Report 2008/013.
Josefsson, S., and I. Liusvaara. n.d. “Edwards-Curve Digital Signature Algorithm (Eddsa).” Request for Comments. RFC 8032; RFC Editor. https://doi.org/10.17487/RFC8032.
Okeya, Katsuyuki, Hiroyuki Kurumatani, and Kouichi Sakurai. 2000. “Elliptic Curves with the Montgomery-Form and Their Cryptographic Applications.” In Proceedings of the Third International Workshop on Practice and Theory in Public Key Cryptography: Public Key Cryptography, 238–57. PKC ’00. London, UK, UK: Springer-Verlag. http://dl.acm.org/citation.cfm?id=648117.746614.